Алгоритм Дугласа-Пекера — это алгоритм, позволяющий уменьшить число точек кривой, аппроксимированной большей серией точек. Алгоритм был независимо предложен Урсом Рамером в 1972 и Давидом Дугласом и Томасом Пекером в 1973. Также алгоритм известен под следующими именами: алгоритм Рамера-Дугласа-Пекера, алгоритм итеративной ближайшей точки и алгоритм разбиения и слияния.
Идея
Суть алгоритма состоит в том, чтобы по данной ломаной, аппроксимирующей кривую, построить ломаную с меньшим числом точек. Алгоритм определяет расхождение, которое вычисляется по максимальному расстоянию между исходной и упрощённой кривыми. Упрощенная кривая состоит из подмножества точек, которые определяются из исходной кривой.
Алгоритм
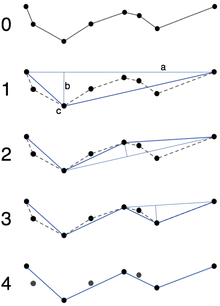
Начальная кривая представляет собой упорядоченный набор точек или линий, и заданное расстояние ε > 0. Начальная кривая показана на рисунке 0, упрощённая — на рисунке 4.
Алгоритм рекурсивно делит линию. Входом алгоритма служат координаты всех точек между первой и последней. Первая и последняя точка сохраняются неизменными. После чего алгоритм находит точку, наиболее удалённую от отрезка, соединяющего первую и последнюю. Если точка находится на расстоянии, меньшем ε, то все точки, которые ещё не были отмечены к сохранению, могут быть выброшены из набора и получившаяся прямая сглаживает кривую с точностью не ниже ε
Если же расстояние больше ε, то алгоритм рекурсивно вызывает себя с на наборе от начальной до данной и от данной до конечной точках (что означает, что данная точка будет отмечена к сохранению).
По окончании всех рекурсивных вызовов выходная ломаная строится только из тех точек, что были отмечены к сохранению.
Псевдокод (рекурсивная реализация)
function DouglasPeucker(PointList[], epsilon) //Находим точку с максимальным расстоянием от прямой между первой и последней точками набора dmax = 0 index = 0 for i = 2 to (length(PointList) - 1) d = PerpendicularDistance(PointList[i], Line(PointList[1], PointList[end])) if d > dmax index = i dmax = d end end //Если максимальная дистанция больше, чем epsilon, то рекурсивно вызываем её на участках if dmax >= epsilon //Recursive call recResults1[] = DouglasPeucker(PointList[1...index], epsilon) recResults2[] = DouglasPeucker(PointList[index...end], epsilon) // Строим итоговый набор точек ResultList[] = {recResults1[1...end-1] recResults2[1...end]} else ResultList[] = {PointList[1], PointList[end]} end // Возвращаем результат return ResultList[] endПсевдокод (итеративная реализация)
function DouglasPeucker(PointList[], epsilon) { // в стек заносим первый и последний индексы stack.push({0, length(PointList) - 1}) // в массиве по заданному индексу храним оставлять точку (true) или нет (false) keep_point[0...length(PointList) - 1] = true while(!stack.empty()) { startIndex = stack.top().first endIndex = stack.top().second stack.pop() dMax = 0 index = startIndex for(i = startIndex + 1 to endIndex - 1) { if(keep_point[i]) { d = PerpendicularDistance(PointList[i], Line(PointList[startIndex], PointList[endIndex])) if(d > dMax) { index = i dMax = d } } } if(dMax >= epsilon) { stack.push({startIndex, index}) stack.push({index, endIndex}) } else { for(j = startIndex + 1 to endIndex - 1) { keep_point[j] = false } } } for(i = 0 to (length(PointList) - 1)) { if(keep_point[i]) { ResultList.Add(PointList[i]) } } return ResultList[] }Применение
Алгоритм применяется для обработки векторной графики и при картографической генерализации.
Кроме того, применяется в робототехнике для обработки результатов работы кругового лазерного дальномера и поэтому также называется алгоритмом разбиения и слияния.
Сложность
Ожидаемая сложность алгоритма может быть оценена выражением T ( n ) = 2 T ( n 2 ) + O ( n ) {displaystyle T(n)=2Tleft({frac {n}{2}} ight)+O(n)} , которая упрощается (как следствие Основной теоремы) в T ( n ) ∈ Θ ( n log n ) {displaystyle T(n)in Theta (nlog n)} . Однако в худшем случае сложность алгоритма O ( n 2 ) {displaystyle Oleft(n^{2} ight)} .